This post gives an outline of the algorithm used to construct an Apollonian gaskel fractal. The full implementation of this Apollonian gasket algorithm and visualisation in C++ is available here.

An Apollonian gasket is a fractal comprising successive layers of tangential but strictly non-intersecting circles, in which a relationship of triples of circles is essential. For the purposes of the implementation, an Appolonian gasket is completely specified by the number of circles at the 0th level of the gasket and number of levels of the gasket; in their theoretical conception, gaskets are structures that consist of infinitely many levels, each of which is self-similar.

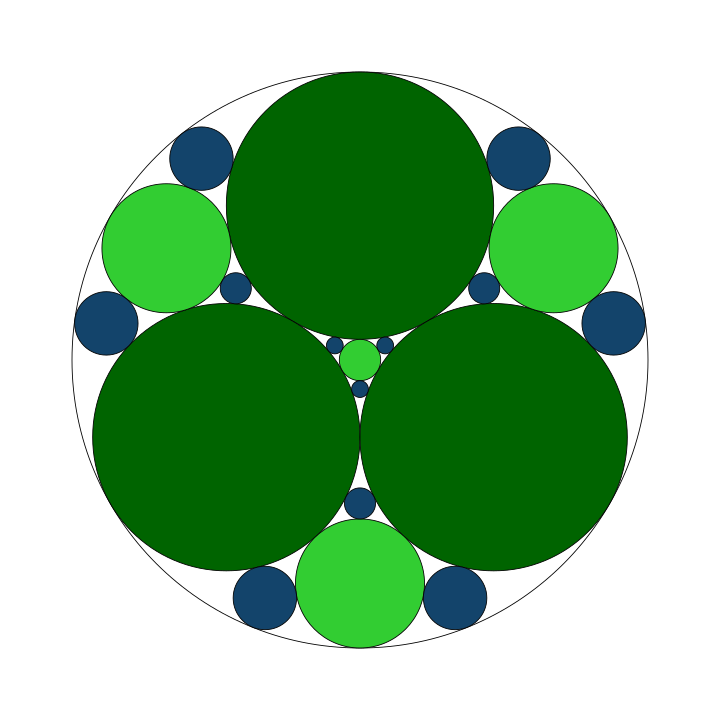
Constructing the 0th layer of the gasket

In either paradigm, the first stage of the gasket involves plotting $n_{zero}$ circles, the first of which contains all of the circles within the structure. The radius of the 0th circle on the 0th level of the gasket may be specified or may without loss of generality be assumed to be equal to 1. Assume that the 0th circle on the 0th level of the gasket has radius $R$. The remaining $n_{zero}-1$ consecutive circles on the 0th level are tangent to each other and the circle that contains them. In fact, each of the $n_{zero}-1$ circles inhabit contiguous sectors of the 0th circle; the angle defining each of the sectors is given by

$$\begin{align*} 2\alpha&=\frac{2\pi}{n_{zero}-1}. \end{align*}$$

Consider the first circle on the 0th level, contained in a sector (any sector may be chosen initially) defined by the angle $2\alpha$. The line bisecting the circle makes an angle of $\alpha$ with the first line that defines the sector. Defining the radius of the first circle as $r$, it follows from trigonometric identities that

$$\begin{align*} \frac{r}{R-r}&=\sin\alpha\\ r&=R\sin\alpha-r\sin\alpha\\ r\left(1+\sin\alpha\right)&=R\sin\alpha\\ r&=\frac{R\sin\alpha}{1+\sin\alpha}. \end{align*}$$

The practical implication is that after any line defining the radius $R$ of the 0th circle is chosen, the center of the first circle is positioned a distance of $R-r$ units away from the center of the 0th circle. The first circle has been shown to have radius $r$. The remaining $n_{zero}-2$ circles on the 0th level are given by rotating the first circle by an angle of $2\alpha$ consecutive times; each consecutive circle has a radius of $r$. The figure below displays the 0th level of a gasket specified with $n_{zero}=4$. The center of the 0th circle is the origin, and the center of the first circle on the 0th level is given by the point $\left(0,R-r\right)$ (this direction was arbitrary).

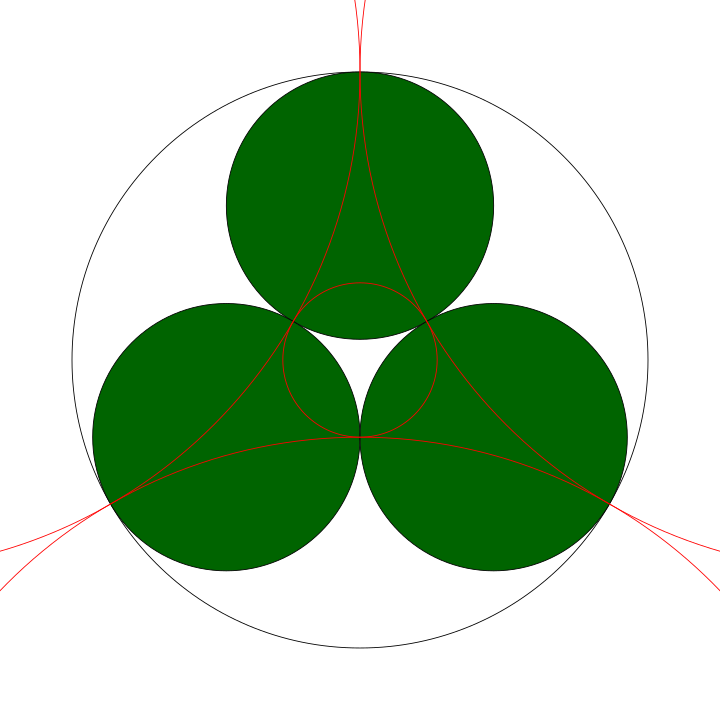
Constructing the reference circles

Once the 0th level of the gasket has been populated, $n_{zero}$ reference circles are defined, which form a crucial part of the algrithm for creating Apollonian gaskets. The 0th reference circle passes through the each point of tangency of the inner circles $1,\ldots,n_{zero}-1$. It is sufficient to consider any three of these points to completely specify the 0th reference circle. The remaining $n_{zero}-1$ reference circles are constructed by considering each pair of consecutive inner circles. The point of tangency between the pair and of each member of the pair with the 0th circle on level 0 (the containing circle) define a triple of points from which the reference circle can be constructed. The figure below gives the plots the reference circles for the gasket specification in the preceding figure.

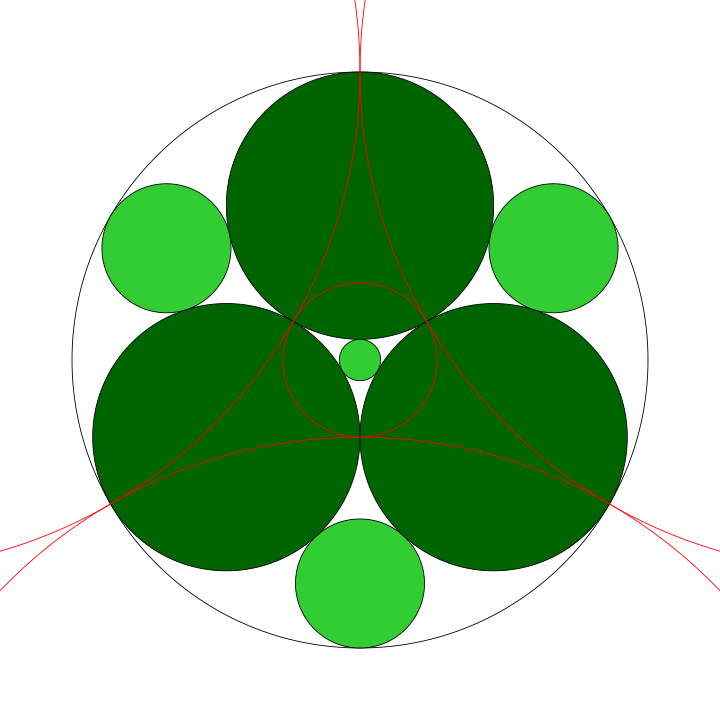
Populating consecutive layers of the gasket

The $n_{zero}$ reference circles are integral to the population of each successive layer of the gasket. The circles on the $n$th layer of the gasket are found by constructing the inverse circles of the each of the circles on the $\left(n-1\right)$th layer of the gasket with respect to the reference circles with which the circles on the $\left(n-1\right)$ layer have empty intersection. There is a special case in the construction of the first layer of the gasket, where the 0th circle completely contains the first reference circle. For this case, the inverse circle of the 0th circle on the 0th level with respect to the 0th reference circle needs to be found.

In general, when constructing the $n$th layer, a method for constructing inverse circles needs to be defined. Inverse circles are constructed from triples of inverse points. To obtain the triple of inverse points, a triple is chosen on one of the circles on layer $n$. Each of these points is then inverted with respect to the appropriate reference circle. For each of the points $\boldsymbol{x}$, the inverse point is obtained according to

$$\begin{align*} \boldsymbol{x}'&=\boldsymbol{x_0}+\frac{r^2(\boldsymbol{x}-\boldsymbol{x_0})}{|\boldsymbol{x}-\boldsymbol{x_0}|^2}, \end{align*}$$

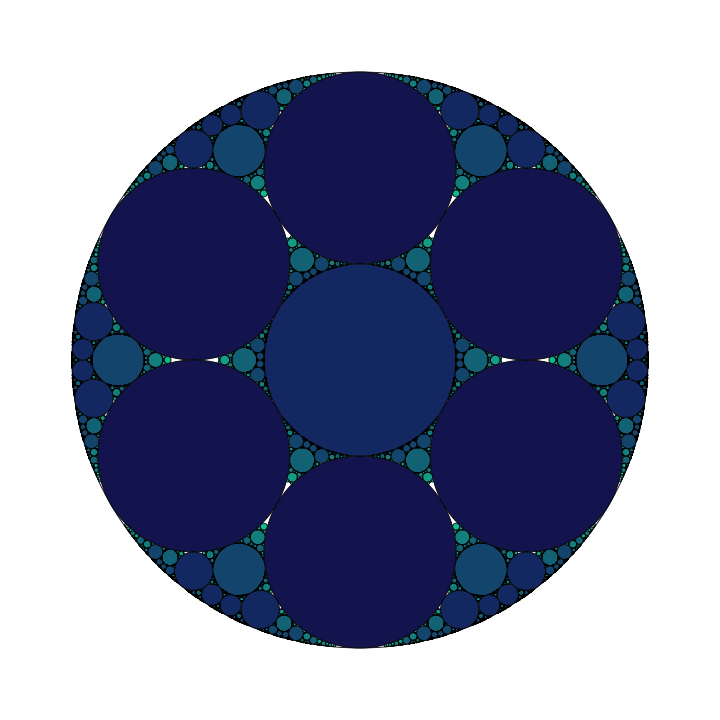
where $\boldsymbol{x}’$ defines the inverse point, $\boldsymbol{x_0}$ defines the center of the reference circle and $r$ defines the radius of the reference circle. The figure below plots the first level of the gasket previously displayed: four inverse circles are calculated relative to the reference circles. This process iterates, and for each level $n$, inverse circles are obtained for only for circles at the $\left(n-1\right)$th level, with respect to the appropriate reference circles. The figure below plots three levels of the gasket, without reference circles.